Beim sogenannten „Damen-Problem (queens problem)“ handelt es sich nicht um eine Story über europäische Königshäuser, sondern um eine schachmathematische Aufgabe. Die klassische Frage beim Damen-Problem lautet: Kann man acht Damen so auf ein Schachbrett stellen, dass keine von diesen eine andere schlagen kann? Und wenn ja, wie viele solcher Stellungen gibt es? Es dürfen also keine zwei Damen auf derselben Reihe, Linie oder Diagonale stehen. Hierbei spielt die Farbe der Damen keine Rolle.
Insgesamt gibt es für das klassische 8×8-Schachbrett mit 8 Damen 92 Lösungen. Diese kann man eventuell auf 12, 6 oder 4 Grund-Lösungen reduzieren, aus denen man die 92 Lösungen durch Transformationen wieder „auffalten“ kann. Vergrößert man das Schachfeld (NxN) und erhöht die verhältnismäßige Anzahl von Damen (Englisch: „Queens“) (N), so nimmt die Rechenkomplexität mit zunehmendem N drastisch zu. Beispiel: Bei N=23 beträgt die Anzahl der möglichen Lösungen unglaubliche 24.233.937.684.440 (24 Billionen).
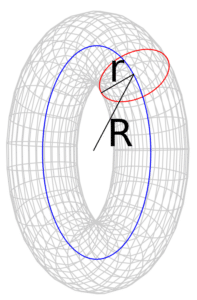
Wem das klassische Damen-Problem nicht anspruchsvoll genug ist, kann sich gerne mit dem „Torus-Damen-Problem“ befassen. Hierbei wird das „Schachfeld“ als Torus, ein mathematisches Objekt aus der Geometrie (s. Abbildung) betrachtet. Die Anzahl der Lösungsmöglichkeiten sinkt dabei um ein Vielfaches.
Einer der klugen Köpfe, die sich mit dem Torus-Damen-Problem auseinandersetzen ist Matthias Engelhardt, ein Mitarbeiter der Lino GmbH. Er hat bereits den T25-, T29- und T31-Wert, also die Lösungsmöglichkeiten für 31 Damen auf dem hypothetischen Torus-Schachfeld errechnet. Aktuell arbeitet er am Ergebnis für T35 und wird vermutlich damit erneut den Weltrekord für das höchste gelöste Torus-Damen-Problem aufstellen – sofern nicht noch ein bisher unbekannter Konkurrent auftaucht und schneller ist!
Die Verbindung zwischen Lino GmbH und Damen-Problem findet sich in der Art und Weise der Lösungsermittlung. Das Damen-Problem stellt ein sogenanntes Constraint Satisfaction Problem (CSP) dar. Diese CSPs sind Kern aller Konfiguratoren, also auch der Tacton Configurator Engine. Die Aufgabe von CSPs ist es, einen Zustand zu finden, der alle aufgestellten Bedingungen (Constraints) erfüllt. Bei diesen ist es üblich, sie mithilfe eines Backtracking-Verfahrens zu bearbeiten.
Hierbei probiert der Rechner alle möglichen Lösungswege und wiederum deren unterschiedliche Verzweigungen durch, bis er auf eine Lösung trifft. Dieser Prozess ist so aufwendig und zeitintensiv, dass das Damen-Problem damit zu einem Benchmark, also einem Vergleichswert, der Leistungsfähigkeit von Rechnern geworden ist. Engelhardts Projekt wird seit April 2020 von der Lino GmbH unterstützt, die Serverkapazität in Nebenzeiten zur Verfügung stellt, damit noch schneller Ergebnisse erzielt werden können. Ansonsten arbeitet Engelhardts privater Rechner daran. Die Suche erfolgt im Hintergrund, sie stört die Arbeit am Rechner kaum und kann bei Bedarf auch unterbrochen und später fortgesetzt werden.
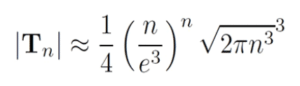
Engelhardt vermutet eine asymptotische Formel für die Torus-N. In dieser Formel steckt mehrfach die Stirling-Formel für n-Fakultät. Mithilfe dieser Formel ist es möglich, das Ergebnis für eine bestimmte Anzahl an Damen ungefähr vorherzusagen. Engelhardts asymptotische Formel kann die Anzahl der Lösungen bis zu 95% genau „vorhersagen“: Für T35 ergibt diese Formel 9,66 Billiarden.
Matthias Engelhardt ist seit 2012 für die Lino GmbH als Senior System Developer und Specialist tätig. Der Diplom-Mathematiker studierte Mathematik an der Universität Erlangen-Nürnberg, sowie der Universität von Konstanz, bevor er unter anderem für Siemens und das IT-Unternehmen Tacton Systems in Stockholm als Entwickler tätig war. Heute ist er als Experte in beratender Funktion im Lino Team tätig und befasst sich in seiner Freizeit mit komplexen mathematischen Fragestellungen wie der des Torus-Damen-Problems.

